松本行弘的程序世界 9 整数和浮点小数
深奥的整数世界
整数是有范围的
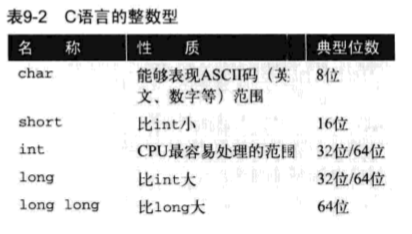
屏幕快照 2018-07-12 下午4.23.38
尝试位运算
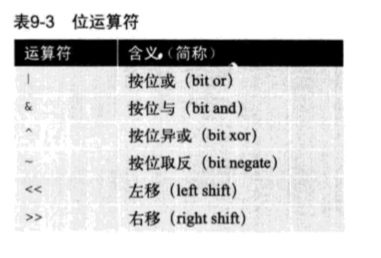
屏幕快照 2018-07-12 下午4.24.58
操作特定的位
位运算组合起来,可以对存储在计算机中的各位进行自由操作。
操作二进制位就等于操作计算机的数据。
基本的位处理操作有4种。
- 取出特定位的状态
- 特定位置位(设为1)
- 特定位清零(设为0)
- 特定位反转
将操作限制在特定位的数为掩码。
表示负数的办法
- 开头一位做符号位
- 将整数的各位反转(1的补数)
Ruby的整数
Ruby的整数有两种,一种是范围有限制的整数Fixnum(32位CPU是31位,64位CPU是63位),另一种是范围没有限制(超过内存容量除外)的整数Bignum,根据计算结果自动变换。
挑战公开密钥方式
RSA加密的强度(解读的困难程度),就归因于素因数分解的难度。
扑朔迷离的浮点小数世界
计算机对小数的处理
固定小数点数不易使用
浮点数,就是小数点的位置可以移动。
科学计数法也有问题
计算机中广泛使用的小数表示方法是科学计数法。科学计数法是指将有效数字和指数组合起来表示小数(实数)。
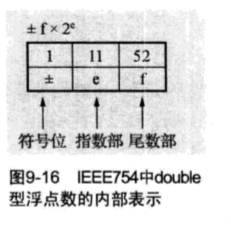
屏幕快照 2018-07-12 下午5.01.23
IEEE754规定,尾数部分的首位始终归一化为1,所以首位始终省略,实质有效数字为53位。
小数不能完全表示
- 计算机中的数的表示有长度(位数)限制。
- 计算机中数的表示是二进制。
浮点数是有限的
浮点数有误差
对于浮点小数,结合法不成立
有不能比较的时候
对于浮点数进行比较运算,只有两个数在内部表示是完全相同的情况下才判定为相等。作为铁则,两个浮点数不能用==进行比较运算。如果有进行比较的必要,判断条件中的两个数的差要足够小。根据操作系统的不同,对于浮点数,足够小的值e有不同的定义。
误差积累
减少运算次数。
不是数的特别“数”

屏幕快照 2018-07-12 下午5.13.14
无限大Inf,零0,非数NaN
计算误差有多种
舍入误差
最大值溢出与最小值溢出
信息丢失
位数脱落
截止误差
误差导致的严重问题
BigDecimal是什么
浮点数运算的陷阱可以归结为:1. 能够表示的精度有限
- 以二进制来表示
Ruby提供了BigDecimal类,有以下3个特点:
- 与Bignum一样,有效数字自动扩展
- 以十进制计算
- 以C语言记述,比内嵌的浮点数类(Float)要慢